2-D to 3-D; 3-D to 2-D

To a visual learner, mathematical nets are easier to visualize and recognize how the 2-D net will fold up into a 3-D shape. Although I would consider myself a visual learner, this activity we did in class was a challenge. In class, we were tasked with creating 3 nets so when they are put together they would form a cube.
In order to complete this task we constructed a triangular prism (half the area of the cube), a triangular pyramid (a third of the area of the cube), and a square pyramid (a sixth of the area of the overall cube). We had to think about how all three of these shapes would fit together to form a cube. 
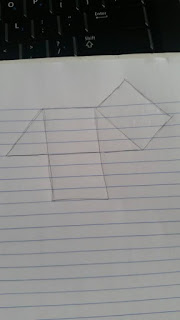
In our group we first started by making the triangular prism (which will account for 1/2 the area of the cube). This was pretty easy to think about and draw out the net because it is our base point. Below is an image of how we drew out our net (left) and a net that we were given at the end of class (right). Comparing the two nets you can see they will make the same 3-D figure. 

                         

After looking at both of these nets, I feel like the way our groups did it was easier to draw out with the least amount of measuring. You can see that to get the rectangle at the top right, we just needed to draw a 2in line that was 90 degrees from the base already created. Where as in the one we were provided after class, you would need to know the exact length of the rectangle, although this wouldn't be difficult to find, it is one extra measurement. This length for a 2in cube would be the square root of three. 

Next, we created the square pyramid. I had a hard time thinking about this one, but once one of my group members drew it out and folded it into the pyramid I had the light bulb moment of where this figure fit in with the triangular prism to form the cube. Also, as a side note, I think this is the coolest net, because it looks like a pinwheel. 

Finally, we made the net for the triangular pyramid. This net was hard to visualize and create. I think what was the hardest about this net was the lengths of the sides and no one side had a full face of the cube. This is due to the fact that it is only 1/6th the area of the cube. Once we created the net and folded it up, it took some time for me to figure out how the shape fit into the other two pieces to form the cube. Once the cube was complete it was a sigh of relief and accomplishment (just like finishing a proof). 

As a class, we shared each of our nets and noticed differences in some, but they all ended up working out. Throughout our discussion someone said "Mathematicians find a solution, prove it, and then accept it, where engineers find the best possible solution," this statement really rang true to me. 
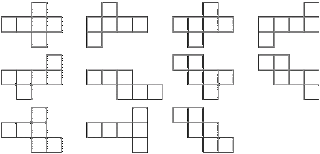
When I first heard this I thought about all the possibilities for a net of a cube. 

In my eyes I feel like the second column, second row net is the most efficient. If you were to draw multiple nets on page you could easily interlock them to get more nets on one page. However, I think the easiest one to visualize that it will get folded up into a cube is the first one. Because you roll up the middle row and then the two extra  side squares make up the base and top surface of the cube. Which one do you like the most?

In the end, everyone thinks and visualizes of things differently. Although, it was hard for me visualize the three pieces of the cube at first in the end I wrapped my brain around it and our cube was complete. Another example that math will stretch your brain and will make you think. 

Doing Math