2-D to 3-D; 3-D to 2-D

To a visual learner, mathematical nets are easier to visualize and recognize how the 2-D net will fold up into a 3-D shape. Although I would consider myself a visual learner, this activity we did in class was a challenge. In class, we were tasked with creating 3 nets so when they are put together they would form a cube.
In order to complete this task we constructed a triangular prism (half the area of the cube), a triangular pyramid (a third of the area of the cube), and a square pyramid (a sixth of the area of the overall cube). We had to think about how all three of these shapes would fit together to form a cube. 
In our group we first started by making the triangular prism (which will account for 1/2 the area of the cube). This was pretty easy to think about and draw out the net because it is our base point. Below is an image of how we drew out our net (left) and a net that we were given at the end of class (right). Comparing the two nets you can see they will make the same 3-D figure. 

                         

After looking at both of these nets, I feel like the way our groups did it was easier to draw out with the least amount of measuring. You can see that to get the rectangle at the top right, we just needed to draw a 2in line that was 90 degrees from the base already created. Where as in the one we were provided after class, you would need to know the exact length of the rectangle, although this wouldn't be difficult to find, it is one extra measurement. This length for a 2in cube would be the square root of three. 

Next, we created the square pyramid. I had a hard time thinking about this one, but once one of my group members drew it out and folded it into the pyramid I had the light bulb moment of where this figure fit in with the triangular prism to form the cube. Also, as a side note, I think this is the coolest net, because it looks like a pinwheel. 

Finally, we made the net for the triangular pyramid. This net was hard to visualize and create. I think what was the hardest about this net was the lengths of the sides and no one side had a full face of the cube. This is due to the fact that it is only 1/6th the area of the cube. Once we created the net and folded it up, it took some time for me to figure out how the shape fit into the other two pieces to form the cube. Once the cube was complete it was a sigh of relief and accomplishment (just like finishing a proof). 

As a class, we shared each of our nets and noticed differences in some, but they all ended up working out. Throughout our discussion someone said "Mathematicians find a solution, prove it, and then accept it, where engineers find the best possible solution," this statement really rang true to me. 
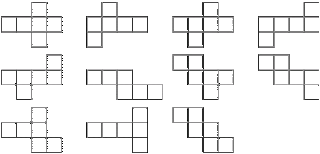
When I first heard this I thought about all the possibilities for a net of a cube. 

In my eyes I feel like the second column, second row net is the most efficient. If you were to draw multiple nets on page you could easily interlock them to get more nets on one page. However, I think the easiest one to visualize that it will get folded up into a cube is the first one. Because you roll up the middle row and then the two extra  side squares make up the base and top surface of the cube. Which one do you like the most?

In the end, everyone thinks and visualizes of things differently. Although, it was hard for me visualize the three pieces of the cube at first in the end I wrapped my brain around it and our cube was complete. Another example that math will stretch your brain and will make you think. 

Doing Math

History of Math Proofs

I can remember back to my Sophomore year in high school, when my Geometry teacher said "Today, we are going to be proving some basic trigonometry concepts." I sat there with a blank look on my face and braced myself. This was the first day in my mathematical career where I will actually be proving a math concept is valid. Previously, I had a lot of trust in my teachers, I believed them that 1+1=2, the area of a rectangle is base times height, and a negative times a negative is actually a positive number. 

Although this task of proving a statement seemed to be daunting, I had a sense of pride, joy, and excitement when I got to the end and finally proved the theorem. This is one of the reasons why I enjoy and appreciate mathematics so much. 

This idea of a proof has dated back 2300 years ago with Euclid. He was the first to formalize the process. This process included "definitions and axioms and then theorems—in that order" (Krantz 5). According to Steven  Krantz article The History and Concept of Mathematical Proof, "A proof is a rhetorical device for convincing another mathematician that a given statement (the theorem) is true" (6). Most of the time we use logical statements within a theorem in which we will prove it is true, this is type dates back to Euclid. However, there are different types of proofs, such as calculations and building a model. 

History of Proofs:

• Babylonians - had diagrams that showed why Pythagoras Theorem was true
• Pythagoreans  (as a society, 569–500 B.C.E.) - discussed that the geometry statements should be proven for validity purpose 
• Eudoxus (408–355 B.C.E.) -  first to use the word theorem and made a collection of these theorems
• Euclid (325–265 B.C.E.) - developed the process of a proof

Euclid, developed this process the correct way. Collect all the definitions and axioms first then come up with a proposition to then prove. Since Euclid, the process that we go about proving a theorem has stayed the same however, we have discovered new definitions and axioms where we can there prove more theorems. The topic of mathematics expands daily. 

Proofs are a beautiful thing. They hold power.  They are a sense of validity in mathematics. They are an intellectual form of communication.  

Although, a proof can be challenging and daunting to take on it has great rewards. From my experience in Geometry in high school to my Senior Math Capstone in college, I appreciate and realize how complex, but yet simple math is. This is all because of proofs. 

Nature of Mathematics Blog 1

What is Math?

Math. A simple four letter word that has a BIG meaning. Many may think math is simply just adding and subtracting two numbers. Although this is considered math, there is more depth to a topic that seems so easy to a typical elementary aged child. 
Since the beginning of time, everyone everyday uses math even without realizing it. Math is a building block that we use throughout our daily lives. As one gets older, the definition of math will grow and unfold more and more. This maybe why answering this daunting question is so difficult. 

Math is a language. Math is a tool. Math is a logical science. 

 Wrapping your brain around a problem, grasping on to solve it, and finally having the celebratory relief of solving the problem are the joys of math. This problem solving process has been around and is how math has come about into a formalize form of science. 

This may not answer the question completely, but it is a start...

To share some of my favorite math accomplishments:
1.  Developing a Counting System
2.  Pythagorean Theorem 
3.  Algebra
4.  Trigonometry
5.  Euler's Method