I would have to admit, I was a bit apprehensive about taking this course. Not because this was my senior capstone course to graduate, but by the title of the course: Nature in Mathematics. This title means history. A word that I am not a huge fan of.
After the first couple of weeks of class, I realized that although we are talking about the history of math, I really enjoyed learning about who and how math was discovered or invented (depending on what you believe).
One topic that we discussed that I will never forget is infinity. We as a class discussed and debated if infinity was a number. If I was a elementary student first seeing the infinity symbol:
∞
I would say that yes, it is a side-ways eight. Although, we all know that infinity is not a side ways eight...it is bigger than the biggest number we know of. Similarly, negative infinity is smaller than the smallest number we know. I believe that infinity is not a number, it is just a symbol representing a limit beyond what we would expect. I believe this because we cannot do operations on infinity and obtain another number. For example, What is infinity*infinity? maybe it is infinity squared, but then what is that?
Another topic within infinity that still blows my mind is the Aristotle's Wheel.
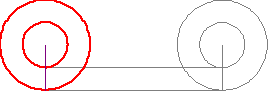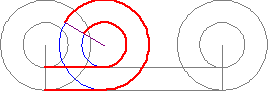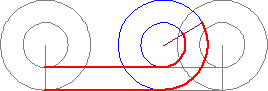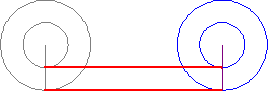
Just like this one day in class talking about infinity, there were multiple other days that I really enjoyed attending. All the topics covered helped me completely understand the topic at hand. Although, I have learned about most the topics before hand in other courses, I only knew the concept, process, why, when, and where you apply it. I did not know where it came from, who originally proved that the topics are true.
Learning the back story behind the topics was eye opening. Some of the mathematicians that we discussed this semester spent most of their lives learning, teaching themselves, and researching math. Mathematicians are truly dedicated to their work. I still think it is crazy that it took Andrew Wiles seven years to complete Fermat's Last Theorem and when written completely out it is over 150 pages long.
Looking at on this semester in class, I really have enjoyed it and feel like I know the concepts and topics more even though we hardly did any math or problems throughout the course. Simply learning about how the concepts became was the icing on the cake for me.
And yes I may like history a little bit more now. :)
Interesting to me as the teacher for sure. I'm a little sad that it didn't feel like we were doing math, but glad that the perspective helped with understanding.
ReplyDeleteProbably needs a bit more for complete - maybe an example where learning about the context helped in understanding the math? But the other Cs are strong as is.